Answer:
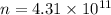
Step-by-step explanation:
It is given that,
Electric field due to the spark,
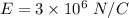
Dimensions of the parallel-plate capacitor is 5.1 cm × 5.1 cm.
The area of the parallel plate,
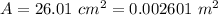
The electric field due to the parallel plate capacitor is given by :
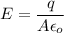
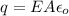
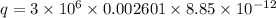
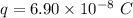
Let n is the number of electrons that must transferred from one plate to the other to create a spark between the plates. It can be calculated as :
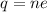
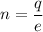
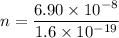
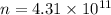
So, the number of electrons must be transferred from one plate to the other is
 . Hence, this is the required solution.
. Hence, this is the required solution.