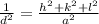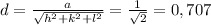Question

Consider a cubic crystal with the lattice constant a. Complete the parts (a)-(c) below. (a) Sketch the crystallographic planes with Miller indices 1 10 and 2 20 . Explain your answer and mark the origin and axes. (b) Explain why these planes are parallel. (c) Find the spacing d between these two planes.

Answer 1

(a) See attachment

(b) The two planes are parallel because the intercepts for plane [220] are X = 0,5 and Y = 0,5 and for plane [110] are X = 1 and Y = 1. When the planes are drawn, they keep the same slope in a 2D plane.

(c)
`d = \frac{a}{\sqrt{h^(2) + k^(2) + l^(2)}} = (1)/(√(2)) =   0,707`

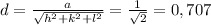
Step-by-step explanation:

(a) To determine the intercepts for an specific set of Miller indices, the reciprocal intercepts are taken as follows:

For [110]

`X = (1)/(1) = 1; Y = (1)/(1) = 1; Z = (1)/(0) = \inf.`

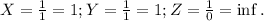
For [220]

`X = (1)/(2) = 0,5;Y = (1)/(2) = 0,5;Z = (1)/(0) = \inf.`

The drawn of the planes is shown in the attachments.

(b) Considering the planes as two sets of 2D straight lines with no intersection to Z axis, then the slope for these two sets are:

For (1,1):

`K_1 = (1)/(1) = 1`

For (0.5, 0.5):

`K_2 = (0.5)/(0.5) = 1`

As shown above, the slopes are exactly equal, then, the two straight lines are considered parallel and for instance, the two planes are parallel also.

(c) To calculate the d-spacing between these two planes, the distance is calculated as follows:

The Miller indices are already given in the statement. Then, the distance is:

`(1)/(d^(2)) = (h^(2) + k^(2) + l^(2))/(a^(2))`

`d = \frac{a}{\sqrt{h^(2) + k^(2) + l^(2)}} = (1)/(√(2)) =   0,707`