Question

134a refrigerant enters an adiabatic compressor at 140kPa and -10C, the refrigerant is compressed at 0.5kW up to 700kPa and 60C. Disregarding changes in kinetic and potential energy. Determine: (a) Isentropic Efficiency (b) The efficiency of the compressor according to the second law Consider the environment at a temperature of 27C

Answer 1

(a) 65.04%

(b) 16.91%

Solution:

As per the question:

At inlet:

Pressure of the compressor, P = 140 kPa

Temperature, T =
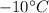`- 10^(\circ)C` = 263 K

Isentropic work, W = 700 kPa

At outlet:

Pressure, P' = 700 kPa

Temperature, T' =
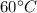`60^(\circ)C` = 333 K

Now, from the steam table;

At the inlet , at a P = 700 kPa, T =
`60^(\circ)C`:

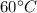h = 243.40 kJ/kg, s = 0.9606 kJ/kg.K

At outlet, at P = 140 kPa, T =
`- 10^(\circ)C`:

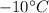h' = 296.69 kJ/kg, s' = 1.0182 kJ/kg.K

Also in isentropic process, s =
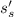`s'_(s)` and
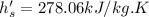`h'_(s) = 278.06 kJ/kg.K` at 700kPa

(a) Isentropic efficiency of the compressor,
`\eta_(s) = (Work\ done\ in\ isentropic\ process)/(Actual\ work\ done)`

`\eta_(s) = (h'_(s) - h)/(h' - h) = frac{278.06 - 243.40}{296.69 - 243.40} = 0.6504 = 65.04%`

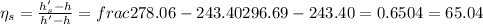
(b) The temperature of the environment,
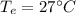`T_(e) = 27^(\circ)C` = 273 + 27 = 300 K

Availability at state 1,
`\Psi = h - T_(e)s = 243.40 - 300* 0.9606 = - 44.78 kJ/kg`

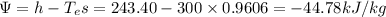
Similarly for state 2,
`\Psi' = h' - T_(e)s' = 296.69 - 300* 1.0182 = - 8.77 kJ/kg`

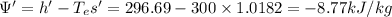
Now, the efficiency of the compressor as per the second law;

`\eta' = (\Psi' - \Psi)/(h' - h) = (- 8.77 - (- 44.78))/(296.69 - 243.40) = 0.6757` = 67.57%