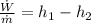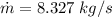Answer:
cycle efficiency: 0.11
steam amount needed: 8.327 kg/s
Step-by-step explanation:
Points 1,2,3 and 4 are depicted in first figure attached. h means enthalpy and s means entropy .
Assumption
Interpolation to get
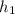 (see second figure)
(see second figure)
p (MPa) h (kJ/kg)
4 3445.3
5
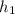
6 3422.2
(3445.3 - 3422.2)/(4 - 6) = (3445.3 -
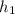 )/(4 - 5)
)/(4 - 5)
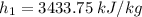
In a similar way
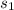 is computed as 6.9852 kJ/(kg K)
is computed as 6.9852 kJ/(kg K)
At 12.35 kPa, i. e., 0.1235 bar (see third figure):
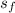 = 0.6922;
= 0.6922;
 = 8.093;
= 8.093;
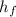 = 205.82 ;
= 205.82 ;
 = 2590.575 (again from interpolation, units omitted)
= 2590.575 (again from interpolation, units omitted)
Quality (x) =
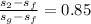
Enthalpy =
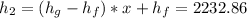
In a similar way
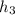 is computed as 205.83 kJ/kg.
is computed as 205.83 kJ/kg.
Point 4 is computed as saturated liquid at 5 MPa; then,
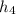 = 1154.2 kJ/kg (see fourth figure).
= 1154.2 kJ/kg (see fourth figure).
Efficiency is calculated as
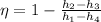
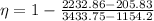
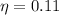
Energy balance at turbine gives