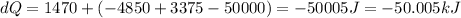Question

A closed system of mass 10 kg undergoes a process during which there is energy transfer by work from the system of 0.147 kJ per kg, an elevation decrease of 50 m, and an increase in velocity from 15 m/s to 30 m/s. The specific internal energy decreases by 5 kJ/kg and the acceleration of gravity is constant at 9.7 m/s^2. Determine the heat transfer for the process, in kJ.

Answer 1

50.005 kJ of heat is transferred by the system

Solution:

As per the question:

Mass of the closed system, m = 10 kg

Decrease in elevation, d = 50 m

Initial velocity, v = 15 m/s

Final velocity, v' = 30 m/s

Change in internal energy, dU = - 5 kJ/kg = - 5000(10 kg) = - 50000 J

As per the first thermodynamics' law:

dQ = dW + (dPE +dKE + dU) (1)

where

dQ = heat transfer change

dPE +dKE + dU = dE = change in the energy of the system

PE = Potential Energy

KE = Kinetic Energy

U = Internal energy

Now,

dPE = mgd = -
`10* 9.7* 50 = 4850 J = - 4.850 kJ`

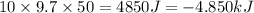
(Since, the elevation decreases and hence PE decreases)

dKE =
`(1)/(2)m(v'^(2) - v^(2)) = (1)/(2)* 10(30^(2) - 15^(2)) = 3375 J = 3.375 kJ`

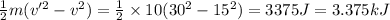
Work done, dW =
`0.147* 10^(3)* 10 = 1470 J`

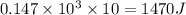
Therefore, using the respective energy values in eqn (1):

`dQ = 1470 + (- 4850 + 3375 - 50000) = - 50005 J = - 50.005 kJ`

Answer 2

-50.005 KJ

Step-by-step explanation:

Mass flow rate = 0.147 KJ per kg

mass= 10 kg

Δh= 50 m

Δv= 15 m/s

W= 10×0.147= 1.47 KJ

Δu= -5 kJ/kg

ΔKE + ΔPE+ ΔU= Q-W

0.5×m×(30^2- 15^2)+ mgΔh+mΔu= Q-W

Q= W+ 0.5×m×(30^2- 15^2) +mgΔh+mΔu

= 1.47 +0.5×1/100×(30^2- 15^2)-9.7×50/1000-50

= 1.47 +3.375-4.8450-50

Q=-50.005 KJ