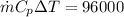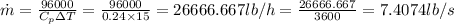Question

A cooling system load is 96,000 BTUh sensible. How much chilled air is required to satisfy the load if the system is designed for a 20°F temperature rise? How much flow is required for 15°F rise?

Answer 1

For
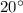`20^(\circ)` - 5.556 lb/s

For
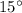`15^(\circ)` - 7.4047 lb/s

Solution:

As per the question:

System Load = 96000 Btuh

Temperature, T =
`20^(\circ)`

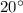
Temperature rise, T' =
`15^(\circ)`

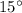
Now,

The system load is taken to be at constant pressure, then:

Specific heat of air,
`C_(p) = 0.24 btu/lb ^(\circ)F`

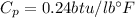
Now, for a rise of
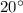`20^(\circ)` in temeprature:

`\dot{m}C_(p)\Delta T = 96000`

`\dot{m} = (96000)/(C_(p)\Delta T) = (96000)/(0.24* 20) = 20000 lb/h = (20000)/(3600) = 5.556 lb/s`

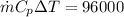
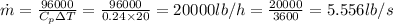
Now, for
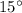`15^(\circ)`:

`\dot{m}C_(p)\Delta T = 96000`

`\dot{m} = (96000)/(C_(p)\Delta T) = (96000)/(0.24* 15) = 26666.667 lb/h = (26666.667)/(3600) = 7.4074 lb/s`