Answer:
h = 37.9 m
Step-by-step explanation:
Assume the height of fuel be h meter in tank
specific gravity of diesel is 0.8
specific gravity of mercury is 13.6
we know rhat density of water is 1000kg/m^3
so density of mercury is
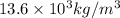
density of mercury is
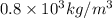
Now equating PRESSURE at AA' position and tank
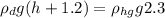
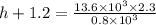
h = 39.1 - 1.2
h = 37.9 m