Step-by-step explanation:
When bullet is shot towards the monkey then let say the distance of monkey from the bullet is "d"
so we can find the time to reach the bullet to the monkey
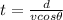
Now similarly we can find the vertical displacement of the bullet in the same time
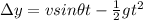
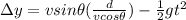
so it is given as
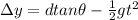
here if the monkey is initially at height H above the ground at given angle then we can say

so we can say that
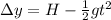
So if at the same time monkey will fall down then the height of monkey from ground after time "t" is given as
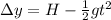
so here bullet will hit the monkey as both monkey and bullet are at same position.