Question

A 900 kg car is accelerated from a speed of 10 m/s to 30 m/s. An estimated heat loss of 20 BTU's occurs during the acceleration. Also, the car increases its elevation by 20m and the internal energy increases by 0.1 kJ/kg. Determine the amount of work that must be done to the system in kJ.

Answer 1

Work = 651,1011 kJ

Step-by-step explanation:

Let´s take the car as a system in order to apply the first law of thermodynamics as follows:

`E_(in)- E_(out)=E_(system,final)- E_(system,initial)`

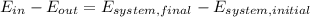
Where

`E_(in)- E_(out)=(Q_(in)-Q_(out))_(heat)+(W_(in)-W_(out))_(work)+(Em_(in)-Em_(out))_(mass)`

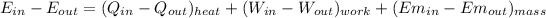
And considering that there is no mass transfer and that the only energy flows that interact with the system are the heat losses and the work needed to move the car we have:

`E_(in)- E_(out)=-Q_(out)+W_(in)`

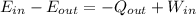
Regarding the energy system we have the following:

`E_(system,final)- E_(system,initial)=(U_(f)-U_(i))_(internal)+(1/2m(V^2_(f)-V^2_(i)))_(kinetic)+(mg(h_(f)-h_(i)))_(potential)`

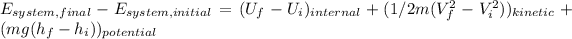
By doing the calculations we have:

`E_(system,final)- E_(system,initial)=[0,1*900]_(internal)+[0,5*900(30^2-10^2)/1000)_(kinetic)+(900*10*(20-0)/1000)_(potential)\\E_(system,final)- E_(system,initial)=90+360+180=630kJ`

Consider that in the previous calculation, the kinetic and potential energy terms were divided by 1.000 to change the units from J to kJ.

Finally, the work needed to move the car under the required conditions is calculated as follows:

`W_(in)=Q_(out)+E_(system,final)- E_(system,initial)\\W_(in)=21,1011+630=651,1011kJ`

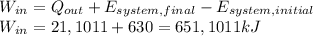
Consider that in the previous calculation, the heat loss was changed previously from BTU to kJ.