Question

Your company has installed a large-area sensing network to manage a chemical plant. In this network, the probability that a message will fail to reach the base station is 0.005. If 2500 messages are sent per day, answer the following questions: (a)What is the probability that fewer than 2485 messages reach the base station? (b)-What is the probability that 7 of the messages fail to reach the base station?

Answer 1

a)P= 0.139

b)P(7)= 0.0352

Step-by-step explanation:

Given that

Number of messages per day ,n= 2500

The probability that a message will fail,p=0.005

Here n is much much larger than the P that is why we will use Poisson distribution

In Poisson distribution

Mean ,λ= n p

λ= 2500 x 0.005

λ=12.5

a)

The probability that fewer than 2485 messages reach the base station =P

`P(x)=(\lambda ^x.e^(-\lambda ))/(x!)`

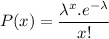
P= 1 - (P(0)+P(1)+P(2) ----------+P(15))

`P(0)=(12.5 ^0.e^(-1.25 ))/(0!)`

`P(1)=(12.5 ^1.e^(-1.25 ))/(1!)`

`P(2)=(12.5 ^2.e^(-1.25 ))/(2!)`

`P(3)=(12.5 ^3.e^(-1.25 ))/(3!)`

`P=1-\left( (12.5 ^0.e^(-1.25 ))/(0!)+(12.5 ^1.e^(-1.25 ))/(1!)+(12.5 ^2.e^(-1.25 ))/(2!) +(12.5 ^3.e^(-1.25 ))/(3!)-----+(12.5 ^(15).e^(-1.25 ))/(15!) \right)`

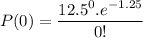
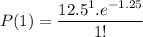
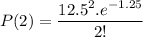
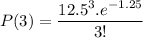
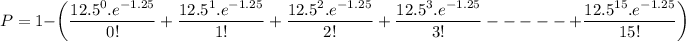
By solving this

P= 0.139

b)

The probability that 7 of the messages fail to reach the base station=P(7)

`P(7)=(12.5 ^7.e^(-1.25 ))/(7!)`

P(7)= 0.0352