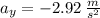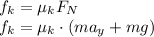Question

A 5.53-kg box is sliding across the horizontal floor of an elevator. The coefficient of kinetic friction between the box and the floor is 0.445. Determine the kinetic frictional force that acts on the box when the elevator is (a) stationary, (b) accelerating upward with an acceleration whose magnitude is 2.92 m/s2, and (c) accelerating downward with an acceleration whose magnitude is 2.92 m/s2.\

Answer 1

The kinetic frictional force when:

a) The elevator is stationary is
`f_(k)=24.12\:N`

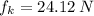
b) The elevator accelerates upward is
`f_(k)=31.30\:N`

c) The elevator accelerates downward is
`f_(k)=16.93\:N`

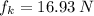
Step-by-step explanation:

Given

`m= 5.53 \:kg\\\mu_k = 0.445`

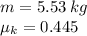
We need to determine the kinetic frictional force when:

• The elevator is stationary
• The elevator accelerates upward
• The elevator accelerates downward

In each of the three cases, the kinetic frictional force is given by
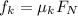`f_(k)=\mu_kF_N`. However the normal force
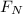`F_N` varies from case to case.

To determine the normal force we can use a Free-body diagram,

The sum of the forces vertically gives us

`\sum F_y=F_N-mg=ma_y`

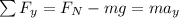
so
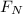`F_N` is

`F_N=ma_y+mg`

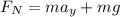
a) When the elevator is stationary, its acceleration is
`a_y= 0 \:(m)/(s^2)`

`f_(k)=\mu_kF_N\\f_(k)=\mu_k\cdot (ma_y+mg)`

`f_(k)=0.445\cdot (5.53\:kg\cdot 0\:(m)/(s^2)+5.53\:kg\cdot 9.80 \:(m)/(s^2) )\\f_(k)=24.12\:N`

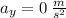
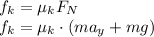
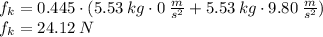
b) When the elevator accelerates upward,
`a_y= +2.92 \:(m)/(s^2)`

`f_(k)=\mu_kF_N\\f_(k)=\mu_k\cdot (ma_y+mg)`

`f_(k)=0.445\cdot (5.53\:kg\cdot 2.92\:(m)/(s^2)+5.53\:kg\cdot 9.80 \:(m)/(s^2) )\\f_(k)=31.30\:N`

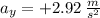
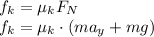
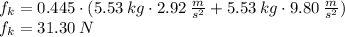
c) When the elevator accelerates downward,
`a_y= -2.92 \:(m)/(s^2)`

`f_(k)=\mu_kF_N\\f_(k)=\mu_k\cdot (ma_y+mg)`

`f_(k)=0.445\cdot (5.53\:kg\cdot -2.92\:(m)/(s^2)+5.53\:kg\cdot 9.80 \:(m)/(s^2) )\\f_(k)=16.93\:N`