Question

A design has an expected distribution of stress with a mean value of 1 MPa and a standard deviation of 0.3 MPa. The strength of the design is expected to have a mean value of 2 MPa and a standard deviation of 0.2 MPa. Both can be assumed to be normal distributions. What is the expected failure rate of the design?

Answer 1

P=0.0028

Step-by-step explanation:

For x:

Mean = 1 MPa

Standard deviation = 0.3 MPa

For y:

Mean = 2 MPa

Standard deviation = 0.2 MPa

Let failure is denoted by F, then F will also follow normal distribution.

F= y-x

Mean

`\mu _F=\mu_y-\mu_x`

`\mu _F=2-1`

`\mu _F=1\ MPa`

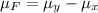
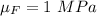
Standard deviation

`\sigma_F=√(\sigma_x^2+\sigma_y^2)`

`\sigma_F=√(0.2^2+0.3^2)`

`\sigma_F=0.36\ MPa`

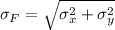
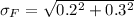
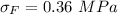
The failure probability given as

`P(F<0)=P\left((0-1)/(0.36) \right)=P(z<-2.77)`

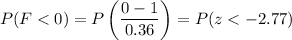
Now from chart P=0.0028