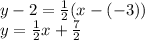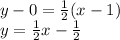Answer:
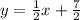
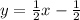
Explanation:
The first step is obtain the derivative of the function y:

(Remember that the slope of the tangent line to any curve is given by its derivative).
Secondly, in order to obtain the equations of the tangent lines parallel to x - 2y = 5 we need to obtain the slope of this line, remember that the line equation is given by:

m : slope
b: y-intercept
Then, the slope of the line
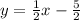
is m = 1/2.
Then, the derivative of the function y must be 1/2:
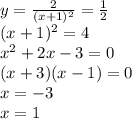
When x = -3, y =(-3-1)/(-3+1)= 2, then one of the tangent lines must pass through the point (-3,2).
When x = 1, y = (1-1)(1+1)= 0, then the other tangent line must pass through the point (1, 0).
Finally, the point-slope equation of a line is given by:
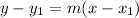
Substituting our previous results we have the equations of the tangent lines: