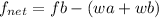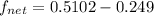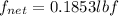Answer:
 {upward}
{upward}
Step-by-step explanation:
Byoncy force is given as


At 60 degree F

R is 1.5 inch = 1.5/12 ft
so solving for Fs we get
fb = 0.5102 lb
By using ideal gas equation calculate mass of air in sphere

p = 200 atm = 2939.19 psi
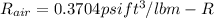
![m = (2939.19 psi a* [(4)/(3) \pi [(1.5)/(12)]^2])/(0.3704 * (90+459.67)](https://img.qammunity.org/2020/formulas/engineering/college/q99f7qsk4xav2f1s7iktudh0lg97wh2hp4.png)
m = 0.1249 lbm
total weight of air and ball os
wa +wb = g(ma+mb)
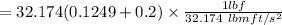
wa+wb = 0.3249 lbf
net foce on the ball is