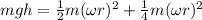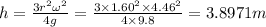Question

Part A A uniform solid disk of radius 1.60 m and mass 2.30 kg rolls without slipping to the bottom of an inclined plane. If the angular velocity of the disk is 4.46 rad/s at the bottom, what is the height of the inclined plane?

Answer 1

Height will be 3.8971 m

Step-by-step explanation:

We have given that radius of the solid r = 1.60 m

Mass of the solid disk m = 2.30 kg

Angular velocity
`\omega =4.46rad/sec`

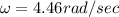
Moment of inertia is given by
`I=(1)/(2)mr^2`

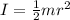
Transnational Kinetic energy is given by
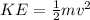`KE=(1)/(2)mv^2` as we know that v =
`v=\omega r`

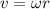
So
`KE=(1)/(2)m(\omega r)^2`

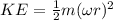
Rotational kinetic energy is given by
`KE_(ROTATIONAL)=(1)/(2)I\omega ^2=(1)/(2)\left ( (1)/(2)mr^2 \right )\omega ^2=(1)/(4)m(r\omega )^2`

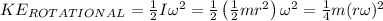
Potential energy is given by mgh

According to energy conservation

`mgh=(1)/(2)m(\omega r)^2+(1)/(4)m(\omega r)^2`

`h=(3r^2\omega ^2)/(4g)=(3* 1.60^2* 4.46^2)/(4* 9.8)=3.8971m`