Answer:
The probability is 0.9106
Explanation:
The variable that says the number of defective toasters follows a binomial distribution, where we have n identical and independent events (50 toasters) with a probability p of success (1% are defective) and a probability 1-p of fail (99% are not defective). So the probability that x toasters from the 50 are defective is:
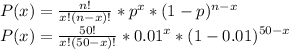
Then, the probability P that no more than one of these toasters is defective is:
P = P(0) + P(1)
So, P(0) and P(1) are calculated as:
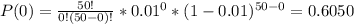
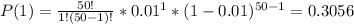
Finally, P is equal to:
P = 0.6050 + 0.3056 = 0.9106