Question

You are the science officer on a visit to a distant solar system. Prior to landing on a planet you measure its diameter to be 1.8×107m and its rotation period to be 22.3 hours . You have previously determined that the planet orbits 2.2×1011m from its star with a period of 407 earth days. Once on the surface you find that the free-fall acceleration is 12.2m/s2.

What is the mass of the Planet?What is the mass of the star?

Answer 1

Mass of the planet = 1.48 × 10²⁵ Kg

Mass of the star = 5.09 × 10³⁰ kg

Step-by-step explanation:

Given;

Diameter = 1.8 × 10⁷ m

Therefore,

Radius =
`\frac{\textup{Diameter}}{\textup{2}}` =
`\frac{\textup{1.8}*10^7}{\textup{2}}`

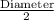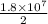
or

Radius of the planet = 0.9 × 10⁷ m

Rotation period = 22.3 hours

Radius of star = 2.2 × 10¹¹ m

Orbit period = 407 earth days = 407 × 24 × 60 × 60 seconds = 35164800 s

free-fall acceleration = 12.2 m/s²

Now,

we have the relation

g =
`\frac{\textup{GM}}{\textup{R}^2}`

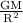
g is the free fall acceleration

G is the gravitational force constant

M is the mass of the planet

on substituting the respective values, we get

12.2 =
`(6.67*10^(-11)* M)/((0.9*10^7)^2)`

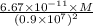
or

M = 1.48 × 10²⁵ Kg

From the Kepler's law we have

T² =
`\frac{\textup{4}\pi^2}{\textup{G}M_(star)}(R_(star))^3`

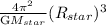
on substituting the respective values, we get

35164800² =
`\frac{\textup{4}\pi^2}{6.67*10^(-11)*M_(star)}(2.2*10^(11))^3`

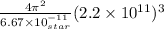
or

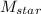`M_(star)` = 5.09 × 10³⁰ kg