Question

A man deposits ​$ 14 comma 14,000 at the beginning of each year for 8 years in an account paying 4​% compounded annually. He then puts the total amount on deposit in another account paying 7​% compounded semiannually for another 7 years. Find the final amount on deposit after the entire 15​-year period.

Answer 1

Value of deposit after 15 years is $264,581.64

Step-by-step explanation:

Given:

Amount deposited every year for 8 years = $14,000

Compound interest rate = 4%

It is an annuity as same amount is deposited every year. Using present value of annuity table to compute the value of deposits at present.

Present value of annuity factor at 4%, 8 years is 6.7327

Present value of deposits = 14,000 × 6.7327

= $94,257.8

This amount is deposited another account earning 7% semi-annually. Annual rate will be 7÷2 = 3.5%

Compounding period is 15×2=30 periods

Value of deposit after 15 years =
`P* (1+i)^(n)`

where, P is present value of deposits that is $94,257.8

i = 0.035

n = 30

Substitute these values in the above formula:

Value of deposit after 15 years =
`94,257.8* (1+0.035)^(30)`

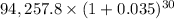
= 94,257.8 × 2.807

= $264,581.64