Answer:
y= 13.475 m
Step-by-step explanation:
Kinematics of the ball : The ball describes a parabolic trajectory.
Because ball move with uniformly accelerated movement in y we apply the following formulas:
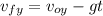 Formula (1)
Formula (1)
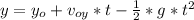 Formula (2)
Formula (2)
Where:
y : vertical position for any time t (m)
y₀ : Initial vertical position (m)
t : time in seconds (s)
 : Initial speed in y (m/s)
: Initial speed in y (m/s)
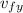 : Final speed in y (m/s)
: Final speed in y (m/s)
g: acceleration due to gravity (m/s)²
Problem development
We apply formula 1 when the ball reaches its maximum height to obtain the initial velocity at y,
 :
:
at maximum height : t= 3 s,
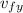 = 0
= 0
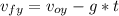
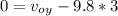
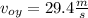
We calculate the requested height using formula 2
t= 3s+2.5s = 5.5 s,
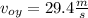 , y₀ = 0
, y₀ = 0
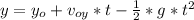
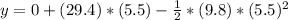
y=13.475 m