Question

A ship maneuvers to within 2.50 x 10^3 m of an islands 1.80 x 10^3 m high mountain peak and fires a projectile at an enemy ship 6.10 x 10^2 m on the other side of the peak. If the ship shoots the projectile with an inital velocity of 2.50 x 10^2 m/s at an angle of 75.0 degrees, how close to the enemy ship does the projectile land? How close (vertically) does the projectile come to the peak?

Answer 1

Step-by-step explanation:

Distance between ship and enemy ship

= 500 + 610

= 3110 m

Range of projectile

R = u² sin2θ / g

= (250x 250 sin 150) / 9.8

= 3188m

The projectile falls within a distance of 3188 - 3110 = 78 m from enemy ship

Height of mountain = 1800 m

We shall find the height of projectile when its horizontal displacement is 2500m

x = 2500 , y = ?

u = 2500 ,

y = x / cos θ - .5 g x² /u²cos² θ

`(2500)/(.2588) - (.5 *9.8*2500*2500)/(250*250*.2588)`

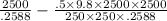
9660 - 7315 m

= 2345 m

It is within 545 m from mountain peak .