Question

An unknown amount of acid can often be determined by adding an excess of base and then back-titrating the excess. A 0.3471−g sample of a mixture of oxalic acid, which has two ionizable protons, and benzoic acid, which has one, is treated with 97.0 mL of 0.1090 M NaOH. The excess NaOH is titrated with 21.00 mL of 0.2060 M HCl. Find the mass % of benzoic acid.

Answer 1

Step-by-step explanation:

The given data is as follows.

Mass of mixture = 0.3471 g

As the mixture contains oxalic acid and benzoic acid. So, oxalic acid will have two protons and benzoic acid has one proton.

This means oxalic acid will react with 2 moles of NaOH and benzoic acid will react with 1 mole of NaOH.

Hence, moles of NaOH in 97 ml =
`(0.1090 * 97)/(1000)`

=
`10.573 * 10^(-3) mol`

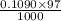
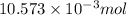
Moles of HCl in 21.00 ml =
`(0.2060 * 21)/(1000)`

=
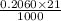
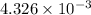`4.326 * 10^(-3)` mol

Therefore, total moles of NaOH that reacted are as follows.

`10.573 * 10^(-3) mol` -
`4.326 * 10^(-3) mol`

=
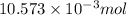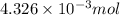
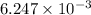`6.247 * 10^(-3)` mol

So, total 3 mole of NaOH will react with 1 mole of mixture. Therefore, number of moles of NaOH reacted with benzoic acid is as follows.

`(6.247 * 10^(-3))/(3)`

=
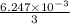
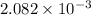`2.082 * 10^(-3)` mol

Since, molar mass of NaOH is 40 g/mol. Therefore, calculate the mass of NaOH as follows.

`2.082 * 10^(-3) mol * 40 g/mol`

=
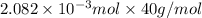
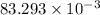`83.293 * 10^(-3)` g

= 0.0832 g

Whereas molar mass of benzoic acid is 122 g/mol.

Therefore, 40 g NaOH = 122 g benzoic acid

So, 0.0832 g NaOH =
`(122 g)/(40 g) * 0.0832 g`

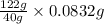
= 0.253 g

Hence, calculate the % mass of benzoic acid as follows.

`(0.253 g)/(0.3471 g) * 100`

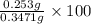
= 73.10%

Thus, we can conclude that mass % of benzoic acid is 73.10%.