Answer:
a) The yearly energy consumption for a US population of 300 million is
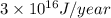
b) The energy that would be released if a 60 kg person were converted entirely into energy is
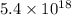 Joules.
Joules.
c) 180 years would this amount of energy support a population of 300 million.
Step-by-step explanation:
a) Average energy consumed by single person of US = 100,000,000 J/year
Then 300 million US citizen will consume:
300 million = 300 × 1,000,000 =

The yearly energy consumption for a US population :
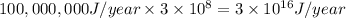
The yearly energy consumption for a US population of 300 million is
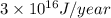
b)
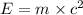
E = Energy from converted mass of m
c = speed of light
Given mass of person = m = 60 kg
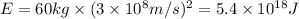
c) Energy calculated in part (b) =
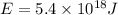
The yearly energy consumption for a US population of 300 million in an year =
Let the that would be supported by
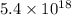 Joules of energy be x.
Joules of energy be x.
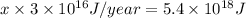
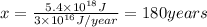
180 years would this amount of energy support a population of 300 million.