Question

(a) Calculate the magnitude of the gravitational force exerted on a 497-kg satellite that is a distance of 1.92 earth radii from the center of the earth. (b) What is the magnitude of the gravitational force exerted on the earth by the satellite? (c) Determine the magnitude of the satellite's acceleration. (d) What is the magnitude of the earth's acceleration?

Answer 1

a) 1321.45 N

b) 1321.45 N

c) 2.66 m/s^2

d) 2.21*10^-22 m/s^2

Step-by-step explanation:

Hello!

First of all, we need to remember the gravitational law:

`F = G (m_1 m_2)/(r^2)`

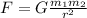
Were

G = 6.67428*10^-11 N(m/kg)^2

m1 and m2 are the masses of the objects

r is the distance between the objects.

In the present case

m1 = earth's mass = 5.9742*10^24 kg

m2 = 497 kg

r = 1.92 earth radii = 1.92 * (6378140 m) = 1.2246*10^7 m

Replacing all these values on the gravitational law, we get:

F = 1321.45 N

a) and b)

Both bodies will feel a force with the same magnitude 1321.45 N but directed in opposite directions.

The acceleration can be calculated dividing the force by the mass of the object

c)

a_satellite = F/m_satellite = ( 1321.45 N)/(497 kg)

a_satellite = 2.66 m/s^2

d)

a_earth = F/earth's mass = (1321.45 N)/( 5.9742*10^24 kg)

a_earth = 2.21*10^-22 m/s^2