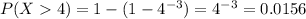Question

An important factor in solid missile fuel is the particle size distribution. Significant problems occur if the particle sizes are too large. From production data in the past, it has been determined that the particle size (in micrometers) distribution is characterized by 3x−4, x > 1, f(x) = 0, elsewhere. (a) Verify that this is a valid density function. (b) Evaluate F(x). (c) What is the probability that a random particle from the manufactured fuel exceeds 4 micrometers?

Answer 1

b)
`F(x)=1-x^(-3)`

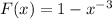
c) 0.0156

Explanation:

Let's call X : '' Particle size (in micrometers) ''

X is a random variable

The distribution function for X is :

`f(x)=3x^(-4)  \\`

For x > 1

f(x) = 0, elsewhere

For a) the condition for f(x) to be a valid density function is that

the integral between -∞ and ∞ of f(x) must be equal to 1.

For the integral I change ∞ for j so ∞ = j

Also for the integral I change -∞ for k so k = -∞

`\int\limits^j_k {f(x)} \, dx =1`

`\int\limits^j_1 {3x^(-4) } \, dx =\\`

`3(j^(-3))/(-3) -3(1^(-3))/(-3) =1`

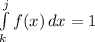
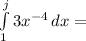
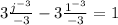
Then f(x) is a valid density function

b) To find F(x) we must integrate between -∞ and x the function f(t)

We calculate f(t) changing x by t in the f(x) function

`x = t \\f(x) =3x^(-4) \\f(t)=3t^(-4)`

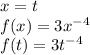
Now we integrate

`\int\limits^x_1 {3t^(-4) } \, dt =-x^(-3)+1`

`F(x)=1-x^(-3)`

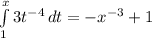
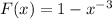
c) P(X>4)

P(X>4) = 1 - P(X≤4)

P(X>4) = 1 - F(4)

`P(X>4) = 1 - (1-4^(-3))=4^(-3)=0.0156`