Question

A spotlight on the ground shines on a wall 12 m away. If a man 2 m tall walks along the x-axis from the spotlight toward the building at a speed of 2 m/s, which is taken as the given dx/dt, how fast is the length of his shadow on the building decreasing when he is 4 m from the building?

Answer 1

dy/dt= 0.6m/s

Step-by-step explanation:

Ok, so we hace two right triangles ABC and ADE which are similar triangles, so we have their corresponding sides like:

`(AD)/(AB)= (DE)/(BC)`

`(8)/(12)= (2)/(Y)`

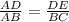
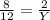
If we consider the distance of the man from the building as x then the distance from the spotlight to the man is 12-x

`(12-x)/(12)= (2)/(y)`

`1-(1)/(12)x= 2*(1)/(y)`

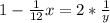
Now we have to take the derivatives of both sides

`-(1)/(12)dx= -2*(1)/(y^2)dy`

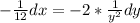
We are now going to divide the hole equation by dt

`(dx)/(dt)=1.6m/s^2`

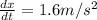
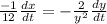`(-1)/(12) (dx)/(dt) = -(2)/(y^2)(dy)/(dt)` and y=3

Let´s sustitute the data on the equation

`-(1)/(12)*(1.6)= (-2)/(9)(dy)/(dt)`

So we have that

`(dy)/(dt) =(1.6)/(12)*(9)/(2)=0.6m/s`