Answer : The moles of
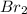 at equilibrium is 0.274 mole.
at equilibrium is 0.274 mole.
Solution :
First we have to calculate the concentration of
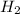 and
and
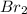 .
.
Concentration of
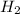 =
=
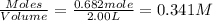
Concentration of
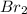 =
=
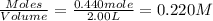
Concentration of
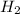 at equilibrium =
at equilibrium =
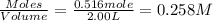
The given equilibrium reaction is,
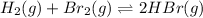
Initially conc. 0.341 0.220 0
At equilibrium. (0.341-x) (0.220-x) 2x
The expression of
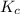 will be,
will be,
![K_c=([HBr]^2)/([H_2][Br_2])](https://img.qammunity.org/2020/formulas/chemistry/high-school/ujd53ii9u2dbu7hgjthj59wvfscqiykmk9.png)
As, the concentration of
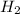 at equilibrium = 0.258 M
at equilibrium = 0.258 M
That means,
0.341 - x = 0.258
x = 0.341 - 0.258
x = 0.083 M
The concentration of
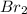 at equilibrium = (0.220-x) = (0.220-0.083) = 0.137 M
at equilibrium = (0.220-x) = (0.220-0.083) = 0.137 M
Now we have to calculate the moles of
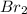 at equilibrium.
at equilibrium.
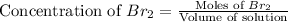
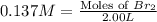
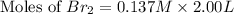
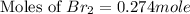
Therefore, the moles of
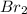 at equilibrium is 0.274 mole.
at equilibrium is 0.274 mole.