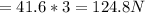Answer:
The magnitud of the force is 124.8N.
Step-by-step explanation:
First we have to find the value of the static friction coefficient, when the external force F is applied to upper block (i will call it A Block) we have a free body diagram as the one shown in the figure i attached, so since this block has no aceleration in any direction the force F should be equal to the friction force between A and B block, one we noticed this we can use the equation for the Friction force to find the coefficient:
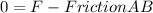
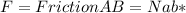 μs
μs
and again, since the block has no acceleration the normal between A and B block should be equal to the weigth of the first block, so we have:

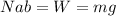
replacing this we have:
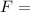 μs
μs
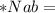 μs*
μs*
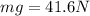
and μs

now it's time to see the free body diagram for the b block, if we now apply the F force to the B block the diagram should look like in the figure.
the color of the arrow gives you an idea of where the force comes from, the blue ones comes from the B block, the red ones from the A block and the brown ones from the ground.
now for the B block you can see two friction forces, one for the ground and one for the A block, both of these directed bacwards, and two normal forces, again one for the ground and one for the A block but the normal force for the A block is aiming downwards.
again we use the fact that the block is not accelerating in any direction so the sum of the forces in x and y direction have to be 0, so:
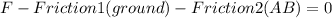
This is the new external F force that we are looking for:
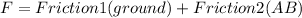
we know Friction2(AB) because we found that in the previous block so:
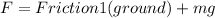 *μs
*μs
for the other friction we have to use the equation:
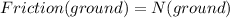 *μs
*μs
from y axis we have:
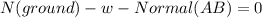
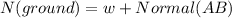
we found the value of Normal(AB) with the previous block so:
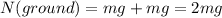
and:
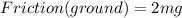 *μs
*μs
 *μs
*μs
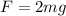 *μs+μs*
*μs+μs*
 *μs
*μs
and since: μs*
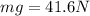
the new F force would be:
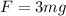 *μs
*μs