Question

C&A purchases fertilizer for its lawn-care business from a supplier who charges $30 per order and $50 per case. Each case consists of five bags of fertilizer. C&A needs 2000 bags of fertilizer a year. C&A's annual holding costs are 30%. What is C&A's holding cost per case per year?

Answer 1

$1.5

Step-by-step explanation:

Given:

Charges per order = $30

Charges per case = $50

1 case = 5 bags of fertilizers

Number of fertilizers bags needed per year = 2000 bags

Annual holding cost, C₀ = 30%

Now,

Annual demand for cases, D =
`\frac{\textup{Number of fertilizers bags needed}}{\textup{Number of bags per case}}`

=
`\frac{\textup{2000}}{\textup{5}}`

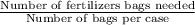
= 400 cases

thus,

Annual unit holding cost per case,
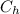`C_h` = 30% of $50 i.e $15

Thus,

Economic Order quantity ( EOQ ) =
`\sqrt{(2C_oD)/(C_h)}`

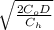
on substituting the respective values, we get

EOQ =
`\sqrt{(2*30*400)/(15)}`

or

EOQ = 40

Now,

Annual ordering cost = Ordering cost × Number of orders

= C₀ ×
`\frac{\textup{annual demand}}{\textup{EOQ}}`

= $30 ×
`\frac{\textup{400}}{\textup{40}}`

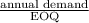
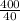
= $300

Annual inventory holding cost

= Annual unit inventory holding cost × Average inventory

=
`C_h` ×
`\frac{\textup{EOQ}}{\textup{2}}`

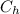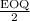
= $15 ×
`\frac{\textup{40}}{\textup{2}}`

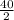
= $300

Now,

Sum of annual ordering and holding cost per case of fertilizer

= $300 + $300

= $600

Therefore,

Annual ordering and holding cost per case of fertiliser

=
`\frac{\textup{600}}{\textup{Annual demand}}`

=
`\frac{\textup{600}}{\textup{400}}`

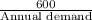
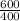
= $1.5