Question

Select the two values of x that are roots of this equation.
2x+11x+15= 0

Answer 1

Answer: x = 3 and = - 5/2

Explanation:

Answer 2

The roots of the equation are x=-3 and x=-2.5

Explanation:

The correct quadratic equation is

2x^2+11x+15=0

we know that

The formula to solve a quadratic equation of the form

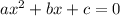`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

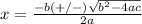
in this problem we have

`2x^(2) +11x+15=0`

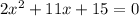
so

`a=2\\b=11\\c=15`

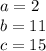
substitute in the formula

`x=\frac{-11(+/-)\sqrt{11^(2)-4(2)(15)}} {2(2)}`

`x=\frac{-11(+/-)√(121-120)} {4}`

`x=\frac{-11(+/-)√(1)} {4}`

`x=\frac{-11(+/-)1} {4}`

`x_1=(-11(+)1)/(4)=-2.5`

`x_2=(-11(-)1)/(4)=-3`

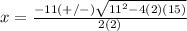
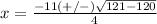
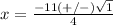
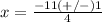
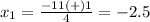
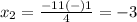
therefore

The roots of the equation are x=-3 and x=-2.5