Question

Say a hacker has a list of n distinct password candidates, only one of which will successfully log her into a secure system. a. If she tries passwords from the list at random, deleting those passwords that do not work, what is the probability that her first successful login will be (exactly) on her k-th try?

Answer 1

The probability is
`(1)/(n)`

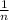
Explanation:

If she has n distinct password candidates and only one of which will successfully log her into a secure system, the probability that her first first successful login will be on her k-th try is:

If k=1

`P = (1)/(n)`

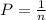
Because, in her first try she has n possibles options and just one give her a successful login.

If k=2

`P=(n-1)/(n) *(1)/(n-1) =(1)/(n)`

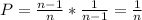
Because, in her first try she has n possibles options and n-1 that are not correct, then, she has n-1 possibles options and 1 of that give her a successful login.

If k=3

`P=(n-1)/(n) *(n-2)/(n-1) *(1)/(n-2) = (1)/(n)`

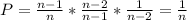
Because, in her first try she has n possibles options and n-1 that are not correct, then, she has n-1 possibles options and n-2 that are not correct and after that, she has n-2 possibles options and 1 give her a successful login.

Finally, no matter what is the value of k, the probability that her first successful login will be (exactly) on her k-th try is 1/n