Question

A manufacturer of matches randomly and independently puts 22 matches in each box of matches produced. The company knows that one-tenth of 5 percent of the matches are flawed. What is the probability that a matchbox will have one or fewer matches with a flaw?

Answer 1

The probability that a matchbox will have one or fewer matches with a flaw is 0.9946 approximately.

Explanation:

Consider the provided information.

A manufacturer of matches randomly and independently puts 22 matches in each box of matches produced. The company knows that one-tenth of 5 percent of the matches are flawed.

One-tenth of 5 percent can be written as 0.5%

Here we have the value of n=22 and the value of p=0.5%=0.005

We want the probability that a matchbox will have one or fewer matches with a flaw.

That means
`P(X\leq 1)=P(X=0)+P(X=1)`

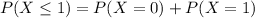
Thus the required probability is:

`P(X\leq 1)=\binom{22}{0}0.005^0(1-0.005)^(22)+\binom{22}{1}0.005^1(1-0.005)^(21)\\P(X\leq 1)=(0.995)^(22)+\binom{22}{1}0.005^1(0.995)^(21)\\P(X\leq 1)\approx 0.8956+22* 0.005* (0.995)^(21)\\P(X\leq 1)=0.8956+0.099\\P(X\leq 1)=0.9946`

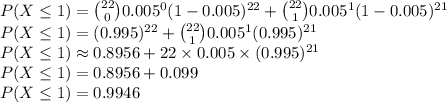
Hence, the probability that a matchbox will have one or fewer matches with a flaw is 0.9946 approximately.