Question

The length of a rectangle is seven inches more than its width. Its area is 78 square inches. Find the width and length of the rectangle.

I'm getting 16 and 23 but my online homework says its wrong

Answer 1

Length: 23.38

Width: 3.34

Explanation:

First I drew out a diagram so that I could visibly see the problem. [ a rectangle with 7x on one side and x on the other.

So to find the area you multiply length time width and 7x times x is 7x^2. The actual area is given: 78, so you set that equal to 7x^2.

Then you want to divide by 7 to get 11.14. Then you want to take the square root of 11.14 to get 3.338 which rounds to 3.34 {try not to round until the very end]. This gives you the width of the rectangle, so to find the length you would have to multiply x by 7 to get 23.38. When you multiply the length and width (3.34 x 23.38) you get 78.08 which can round to 78.

7x^2 = 78

x^2 = 78/7

x^2= 11.142...

x = sqrt(1.142...)

x = 3.338 --> 3.34 --> width

3.34 x 7 --> 23.38 --> length

3.34 x 23.38 --> 70.8

Answer 2

Width = 6 inches

Length = 13 inches

Explanation:

The length of a rectangle is seven inches more than its width. Its area is 78 square inches.

Let w be the width of the rectangle

length is w+7

Area of the rectangle is length time width

`area=w(w+7)`

`78=w(w+7)`

`78=w^2+7w`

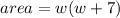
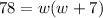
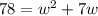
Subtract 78 from both sides

`0=w^2+7w-78`

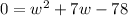
now factor it and solve for w

product is -78 and sum is +7

`0=w^2+7w-78`

`0=(w+13)(w-6)`

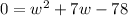
Set each factor =0 and solve for x

`w+13=0, so w=-13`

`w-6=0, so w=6`

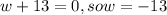
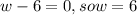
width cannot be negative , so the value of w is 6

Width = 6 inches

Length = width +7=13 inches