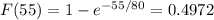Question

The time to​ failure, t, in​ hours, of a machine is often exponentially distributed with a probability density function ​f(t) = k e^(-kt)​, 0 to infinity​, where k= 1/a and a is the average amount of time that will pass before a failure occurs. Suppose that the average amount of time that will pass before a failure occurs is 80 hr. What is the probability that a failure will occur in 55 hr or​ less?

Answer 1

The probability is 0.4972

Explanation:

The probability density function for the time of failure is:

f(t) = k e^(-kt)​

Where k=1/a and a = 80hr so f(t) is equal to:

`f(t)=(1)/(a)e^{(-t)/(a) }`

`f(t)=(1)/(80)e^{(-t)/(80) }`

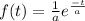
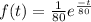
Then, if the probability density function follow a exponential distribution, the probability distribution function is:

`F(t)=1-e^(-t/a)`

`F(t)=1-e^(-t/80)`

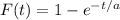
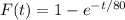
The probability distribution function give as the probability that a failure will occur in t hours or less, so the probability that a failure will occur in 55 hr or​ less is calculated as:

`F(55)=1-e^(-55/80)=0.4972`