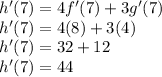Question

Suppose f(7) = 5​, f'(7) = 8​, g(7) = 3​, and g'(7) = 4. Find h(7) and h'(7)​, where h(x ) = 4f (x) + 3g(x).

Answer 1

h(7) = 29

h'(7) = 44

Explanation:

If
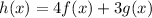`h(x) =4f(x)+3g(x)`, to find h(7) we can substitute the values of f(7) and g(7) and we get:

`h(7)=4f(7)+3g(7)\\h(7)=4(5)+3(3)\\h(7)=20+9\\h(7)=29`

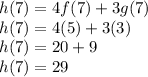
To find the derivative, we know that the derivative of a sum of functions equals the sum of the derivatives of those functions.

This would mean that
`h'(x)=4f'(x)+3g'(x)`, we can substitute the values for f'(7) and g'(7)

`h'(7)=4f'(7)+3g'(7)\\h'(7)=4(8)+3(4)\\h'(7)=32+12\\h'(7)=44`