Answer:
The ratio of asteroid-A’s acceleration to asteroid-B’s acceleration is 37:7800.
Step-by-step explanation:
Mass of asteroid-A = m =
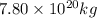
Mass of asteroid-B = m' =
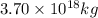
As we know , Force = mass × Acceleration
1) Force on an asteroid-A
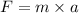
where , a is the acceleration due to force applied on asteroid-A
2) Force on an asteroid-B
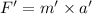
where , a' is the acceleration due to the force applied on asteroid-B
Same force is exerted on the both the asteroids say F.
F = F'
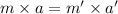
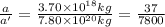
The ratio of asteroid-A’s acceleration to asteroid-B’s acceleration is 37:7800.