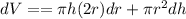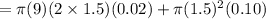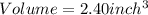Question

The volume V of a solid right circular cylinder is given by V = πr2h where r is the radius of the cylinder and h is its height. A soda can has inner radius r = 1.5 inches, height h = 9 inches, wall thickness 0.02 inches, and top and bottom thickness 0.05 inches. Use linearization to compute the volume, in in3, of metal in the walls and top and bottom of the can. Give your answer to 2 decimal places.

Answer 1

`Volume = 2.40 inch^3`

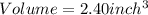
Explanation:

Given data:

inner radius of can 1.5 inch

height of can 9 inch

thickness of can dr = 0.02 inch

top and bottom thickness 0.05 inch

so dh = 0.05+ 0.05 = 0.10 inch

we know that

`volume =\pi r^2 h`

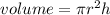
By using total differentiation method we have

`dV = (\partial V)/(\partial r) dr + (\partial V)/(\partial h) dh`

`= (\partial (\pi r^2 h) )/(\partial r) dr + (\partial (\pi r^2 h))/(\partial h) dh`

`=\pi h(\partial (r^2))/(\partial r) dr +  \pi r^2(\partial h)/(\partial h) dh`

`= \pi h(2r) dr + \pi r^2 dh`

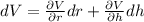
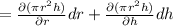
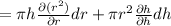
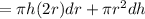
puttinfg all value to get required value of volume

`dV = = \pi h(2r) dr + \pi r^2 dh`

`= \pi (9)(2* 1.5)(0.02)+ \pi (1.5)^2 (0.10)`

`Volume = 2.40 inch^3`