Question

Eight books are placed on a shelf. Three of them form a 3-volume series, two form a 2-volume series, and 3 stand on their own. In how many ways can the eight books be arranged so that the books in the 3-volume series are placed together according to their correct order, and so are the books in the 2-volume series?

Answer 1

Answer:480 ways

Step-by-step explanation:

Given

There are 3-Volume series i.e.

`V_1,V_2,V_3`

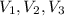
No of ways in which they can be arranged in order is 2 i.e.
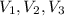`V_1,V_2,V_3` or
`V_3,V_2,V_1`

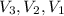
For 2 volume series

There are two ways in which 2 volume series is arranged

`V_1,V_2 or V_2,V_1`

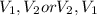
Considering 3 volume books to be a single book denoted by a

and 2 volume books to be a single denoted by b

Thus we have to arrange a,b and 3 others books

No of ways in which 5 books can be arranged is 5!

also a and b can be arranged in two ways internally so

there are total of =
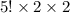`5!* 2* 2`=480 ways