Answer:
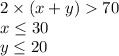
c) (35,20) and (25,15)
Explanation:
We are given the following information in the question:
Let x be the length of the rectangle and y be the width.
Perimeter of rectangle =

a) Then, we can have the following inequalities:
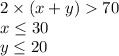
b) The attached image shows the graph for the three inequalities.
c) The two possible combination of length and width of rectangle could be:
(35,20) and (25,15)
The points are shown in the graph and satisfies all the three inequalities.