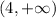Question

What are the domain and range of the function f(x)=113(x-5)²+4

Answer 1

The domain and range of the given function are
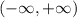`(-\infty,+\infty)` and
`(4,+\infty)`

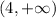
Solution:

Given, function is f(x) =
`113(x-5)^(2)+4`

f(x) is a polynomial, so there exists no value of x, such that the function becomes undefined, which means the domain of the given function extends from
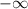`-\infty` to
`+\infty`

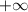
Domain of f(x) =
`(-\infty,+\infty)`

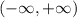
Now, we need to find the range of f(x).

f(x) =
`113(x-5)^(2)+4` .Here, x is in square term (i.e.
`(x-5)^(2)` )

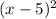So for any range of values of x, the value of
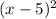`(x-5)^(2)` will always be in the range of 0 to ∞

Numerical term 113 which is product with
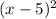`(x-5)^(2)` will have no effect on range.

Because
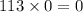`113 * 0 = 0` and so the range of function is still 0 to ∞

Second numerical term 4 which is in addition with
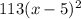`113(x-5)^(2)` will change the range of function.

Because, 0 + 4 = 4, and ∞ + 4 = ∞

So, the range of the given function f(x) is 4 to ∞

Hence the domain and range of the given function are
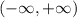`(-\infty,+\infty)` and
`(4,+\infty)`