Question

asked Dec 8, 2020 112k views

1 Answer

Sammitch · Answer 1 · 2020-12-15T10:07:55+0000

Answer:

a) There is a 98.17% probability that a randomly selected page has at least one typo on it.

b) There is a 9.16% probability that a randomly selected page has at most one typo on it.

Explanation:

Since we only have the mean, we can solve this problem by a Poisson distribution.

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

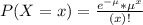
$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

In which

x is the number of sucesses

e = 2.71828 is the Euler number

$\mu$ is the mean in the given time interval.

In this problem, we have that
$\mu = 4$

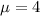
(a) What is the probability that a randomly selected page has at least one typo on it?

Thats is
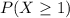$P(X \geq 1)$ . Either a number is greater or equal than 1, or it is lesser. The sum of the probabilities must be decimal 1. So:

$P(X < 1) + P(X \geq 1) = 1$

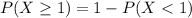
$P(X \geq 1) = 1 - P(X < 1)$

In which

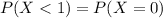P(X < 1) = P(X = 0) .

So

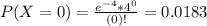
P(X = 0) = (e^(-4)*4^(0))/((0)!) = 0.0183

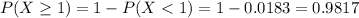
$P(X \geq 1) = 1 - P(X < 1) = 1 - 0.0183 = 0.9817$

There is a 98.17% probability that a randomly selected page has at least one typo on it.

(b) What is the probability that a randomly selected page has at most one typo on it?

This is
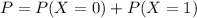P = P(X = 0) + P(X = 1) . So:

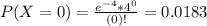
P(X = 0) = (e^(-4)*4^(0))/((0)!) = 0.0183

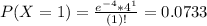
P(X = 1) = (e^(-4)*4^(1))/((1)!) = 0.0733

P = P(X = 0) + P(X = 1) = 0.0183 + 0.0733 = 0.0916

There is a 9.16% probability that a randomly selected page has at most one typo on it.

Please log in or register to add a comment.