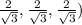Answer:
Explanation:
Let the rectangle have (x,y,z) as vertex in positive octant. The rectangular box has to be necessarily symmetrical about all the three axes.
Then the sides of the box would be
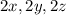
Volume =
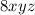
Maximize volume subject to
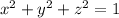
i.e.
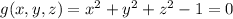
Use Lagrangian multipliers , we have
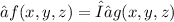 at the maximum
at the maximum
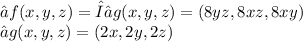
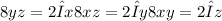
Dividing we get

Similarly
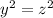
Thus we get
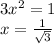
Hence dimensions are
(2x,2y,2z)
So dimensions are