Question

A machine that produces ball bearings has initially been set so that the true average diameter of the bearings it produces is .500 inches. A bearing is acceptable if its diameter is within .004 inches of this target value. Suppose, however, that the setting has changed during the course of production, so that the bearings have normally distributed diameters with mean value .499 inches and standard deviation .002 inches. What percentage of the bearings produced will not be acceptable?

Answer 1

7.3% percentage of the bearings produced will not be acceptable.

Explanation:

Consider the provided information.

Average diameter of the bearings it produces is .500 inches. A bearing is acceptable if its diameter is within .004 inches of this target value.

Let X is the normal random variable which represents the diameter of bearing.

Thus, 0.500-0.004<X<0.500+0.004

0.496<X<0.504

The bearings have normally distributed diameters with mean value .499 inches and standard deviation .002 inches.

Use the Z score formula:
`(X-\mu)/(\sigma)`

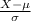
Therefore

`(0.496-0.499)/(0.002)\leq z\leq (0.504-0.499)/(0.002)`

`(-0.003)/(0.002)\leq z\leq (0.005)/(0.002)`

`-1.5\leq z\leq 2.5`

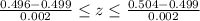
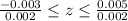
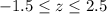
Now use the standard normal table and determine the probability of that a ball bearing will be acceptable.

`P(-1.5\leq z\leq 2.5)=0.9938-0.0668=0.9270`

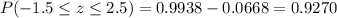
We need to find the percentage of the bearings produced will not be acceptable.

So subtract it from 1 as shown.

1-0.9270=0.073

Hence, 7.3% percentage of the bearings produced will not be acceptable.