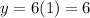Question

Direct variation worksheet

Answer 1

Part 4) k=1/2

Part 5) k=-2/3

Part 6) y=32

Part 7) x=6

Part 8) v=99

Part 9)b=6

Part 10) y=6

Explanation:

we know that

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
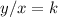`y/x=k` or
`y=kx`

In a proportional relationship the constant of proportionality k is equal to the slope m of the line and the line passes through the origin

Part 4) Find the value of the constant of proportionality k

we have

`y=(1)/(2)x`

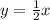
Remember that the value of k is the same that the value of the slope

`m=(1)/(2)`

so

`k=(1)/(2)`

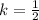
Part 5) Find the value of the constant of proportionality k

we have

`y=-(2)/(3)x`

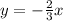
Remember that the value of k is the same that the value of the slope

`m=-(2)/(3)`

so

`k=-(2)/(3)`

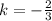
Part 6) Suppose that y varies directly with x, and y=16 when x=8. Find y when x=16

step 1

Find the value of the constant of proportionality k

`k=y/x`

`k=16/8=2`

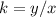
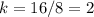
step 2

Find the equation of the direct variation

`y=kx`

substitute the value of k

`y=2x`

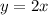
step 3

Find y when x=16

`y=2(16)=32`

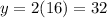
Part 7) Suppose that y varies directly with x, and y=21 when x=3. Find x when y=42

step 1

Find the value of the constant of proportionality k

`k=y/x`

`k=21/3=7`

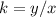
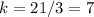
step 2

Find the equation of the direct variation

`y=kx`

substitute the value of k

`y=7x`

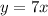
step 3

Find x when y=42

`42=7x`

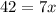
solve for x

`x=42/7`

`x=6`

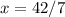
Part 8) Suppose that v varies directly with g, and v=36 when g=4. Find v when g=11

step 1

Find the value of the constant of proportionality k

`k=v/g`

`k=36/4=9`

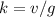
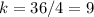
step 2

Find the equation of the direct variation

`v=kg`

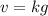
substitute the value of k

`v=9g`

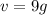
step 3

Find v when g=11

`v=9(11)=99`

Part 9) Suppose that a varies directly with a, and a=7 when b=2. Find b when a=21

step 1

Find the value of the constant of proportionality k

`k=a/b`

`k=7/2=3.5`

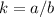
step 2

Find the equation of the direct variation

`a=kb`

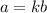
substitute the value of k

`a=3.5b`

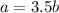
step 3

Find b when a=21

`21=3.5b`

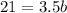
solve for b

`b=21/3.5`

`b=6`

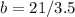
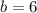
Part 10) Suppose that y varies directly with x, and y=9 when x=3/2. Find y when x=1

step 1

Find the value of the constant of proportionality k

`k=y/x`

`k=9/(3/2)=6`

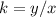
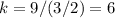
step 2

Find the equation of the direct variation

`y=kx`

substitute the value of k

`y=6x`

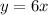
step 3

Find y when x=1

`y=6(1)=6`