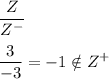Question

Suppose ℤ denotes the set of all integers, ℤ+ denotes the set of all positive integers, and ℤ− denotes the set of all negative integers. Similarly ℝ denotes the set of all real numbers, ℝ+ denotes the set of all positive real numbers, and ℝ− denotes the set of all negative real numbers. Suppose ℕ denotes the set of all natural numbers and ℚ denotes the set of all rational numbers. Enter "T" for each true, and "F" for each false statements.(a) Z / Q = Z(b) Z / Z- = Z+

Answer 1

a) False

b) False

Explanation:

We are given the following information in the question:

`Z` denotes the set of all integers.

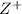`Z^+` denotes the set of all positive integers.

`Z^-` denotes the set of all negative integers.

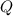`Q` denotes the set of all rational numbers

a) False

We will give a counter example .

`\displaystyle(Z)/(Q)\\\\\displaystyle(3)/((2)/(3)) = \displaystyle(9)/(2) \\otin Z`

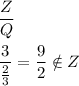
b) False

We will give a counter example .

`\displaystyle(Z)/(Z^-)\\\\\displaystyle(3)/(-3) = -1 \\otin Z^+`