Question

The student council is hosting a drawing to raise money for scholarships. They are selling tickets for $1 each and will sell 1500 tickets. There is one $600 grand prize, five $50 second prizes, and twenty $25 third prizes. You just bought a ticket. Find the expected value for your profit. Round your answer to the nearest cent (two decimal points).

Answer 1

The expected value for your profit is -$0.10

Explanation:

The expected value of a discrete variable is calculated as:

`E(x)=x_1p(x_1)+x_2p(x_2)+...+x_np(x_n)`

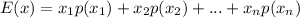
Where,
`x_1, x_2` and
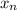`x_n` are the values that the variable can take and
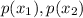`p(x_1), p(x_2)` and
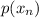`p(x_n)` are their respective probabilities.

So, the expected value of your income is:

`E(x)=600(1/1500)+50(5/1500)+25(20/1500)+0(1474/1500)`

`E(x)=0.9`

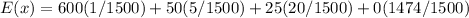
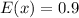
Because, you can win $600 with a probability of 1/1500, $50 with a probability of 5/1500, $25 with a probability of 20/1500 or $0 with a probability of 1474/1500.

Then, if you buy a ticket for $1, the expected value for your profit is:

Expected Value = Expected Income - Cost

Expected Value = $0.9 - $1

Expected Value = -$0.1