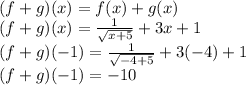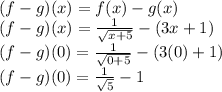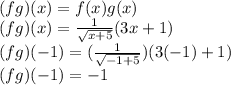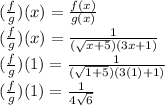Answer:
a.
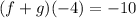
b.
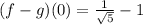
c.
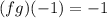
d.
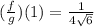
Explanation:
Given that:
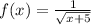
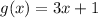
The sum, rest, multiplication or division of functions are calculated as following:
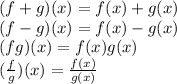
For values of x where f(x) and g(x) are defined and in the case of
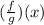 for values of g(x) different from zero.
for values of g(x) different from zero.
Taking into account that f(x) and g(x) are defined for values of x equals to -4, 0, 1 and -1 and g(1) is different from zero, we get: