Question

A pipeline (NPS = 14 in; schedule = 80) has a length of 200 m. Water (15℃) is flowing at 0.16 m3/s. What is the pipe head loss for the water supply over a distance of 200 m? Hint: Use an iterative approach for the empirical equation.

Answer 1

Head loss is 1.64

Step-by-step explanation:

Given data:

Length (L) = 200 m

Discharge (Q) = 0.16 m3/s

According to table of nominal pipe size , for schedule 80 , NPS 14, pipe has diameter (D)= 12.5 in or 31.8 cm 0.318 m

We know,
`head\ loss  = (f L V^2)/(( 2 g D))`

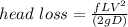
where, f = Darcy friction factor

V = flow velocity

g = acceleration due to gravity

We know, flow rate Q = A x V

solving for V

`V = (Q)/(A)`

`= (0.16)/((\pi)/(4) (0.318)^2) = 2.015 m/s`

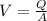
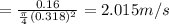
obtained Darcy friction factor

calculate Reynold number (Re) ,

`Re = (\rho V D)/(\mu)`

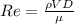
where,
`\rho` = density of water

`\mu` = Dynamic viscosity of water at 15 degree C = 0.001 Ns/m2

so reynold number is

`Re = (1000* 2.015* 0.318)/(0.001)`

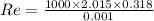
= 6.4 x 10^5

For Schedule 80 PVC pipes , roughness (e) is 0.0015 mm

Relative roughness (e/D) = 0.0015 / 318 = 0.00005

from Moody diagram, for Re = 640000 and e/D = 0.00005 , Darcy friction factor , f = 0.0126

Therefore head loss is

`HL = (0.0126 (200)(2.015)^2)/(( 2 * 9.81 * 0.318))`

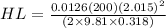
HL = 1.64 m