Question

You and a friend play a game where you each toss a balanced coin. If the upper faces on the coins are both tails, you win $1; if the faces are both heads, you win $6; if the coins do not match (one shows a head, the other a tail), you lose $3 (win (−$3)). Calculate the mean and variance of Y, your winnings on a single play of the game. Note that E(Y) > 0.

Answer 1

Answer: The mean and variance of Y is $0.25 and $6.19 respectively.

Explanation:

Given : You and a friend play a game where you each toss a balanced coin.

sample space for tossing two coins : {TT, HT, TH, HH}

Let Y denotes the winnings on a single play of the game.

You win $1; if the faces are both heads

then P(Y=1)=P(TT)=
`(1)/(4)=0.25`

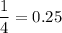
You win $6; if the faces are both heads

then P(Y=6)=P(HH)=
`(1)/(4)=0.25`

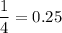
You loose $3; if the faces do not match.

then P(Y=1)=P(TH, HT)=
`(2)/(4)=0.50`

The expected value to win : E(Y)=
`\sum_(i=1)^(i=3) y_ip(y_1)`

`=1*0.25+6*0.25+(-3)*0.50=0.25`

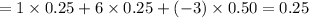
Hence, the mean of Y : E(Y)= $0.25

`E(Y^2)=\sum_(i=1)^(i=3) y_i^2p(y_i)\\\\=1^2*0.25+6^1*0.25+(-3)^2*0.5\\\\=0.25+1.5+4.5=6.25`

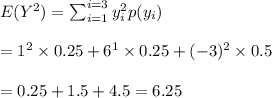
Variance =
`E[Y^2]-E(Y)^2`

`=6.25-(0.25)^2=6.25-0.0625=6.1875\approx6.19`

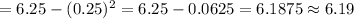
Hence, variance of Y = $ 6.19