Question

The temperature at a point (x, y) is T(x, y), measured in degrees Celsius. A bug crawls so that its position after t seconds is given by x = 2 + t , y = 3 + 1 2 t, where x and y are measured in centimeters. The temperature function satisfies Tx(2, 4) = 8 and Ty(2, 4) = 9. How fast is the temperature rising on the bug's path after 2 seconds? (Round your answer to two decimal places.)

Answer 1

The temperature is increasing at the rate of 6.5 degree celcius per second.

Explanation:

We are given the following information:

Temperature of a point is given by T(x,y)

After t seconds a bug reaches a point
`x = √(2 + t), y = 3 + (1)/(2)t`

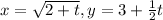
At t = 2, x = 2, y = 4

The temperature function satisfies:

`T_x(2,4) = 8\\T_y(2,4) = 9`

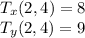
We have to find:

`\displaystyle(dT)/(dt) = T_t(x(t), y(t))\\\\= T_x(x(t),y(t)).x'(t) + T_y(x(t),y(t)).y'(t) \\\\= T_x(x(t),y(t)).\displaystyle(1)/(2√((t+2))) + T_y(x(t),y(t)).\displaystyle(1)/(2) \\\\\displaystyle(dT(x,y))/(dt)_(at~t=2) = \displaystyle(dT(2,4))/(dt)_(at~t=2) = 8.\displaystyle(1)/(4) + 9.\displaystyle(1)/(2) = 2 + 4.5 = 6.5`

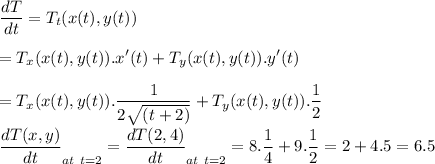
Hence, the temperature is increasing at the rate of 6.5 degree celcius per second.