Question

You plan on making a $235.15 monthly deposit into an account that pays 3.2% interest, compounded monthly, for 20 years. At the end of this period, you plan on withdrawing regular monthly payments. Determine the amount that you can withdraw each month for 10 years, if you plan on not having anything in the account at the end of the 10 year period and no future deposits are made to the account. a. $769.27 b. $767.23 c. $78,910.41 d. $79,120.84 Please select the best answer from the choices provided A B C D

Answer 1

its A (ik that it was already answered and it was posted over a year ago but i wanted the points)

Answer 2

Ans. a) $769.27 is the amount of money that you can withdraw every month for 120 months at a rate of 3.2% compounded monthly if you deposit $235.15 every month, for 20 years.

Step-by-step explanation:

Hi, first we have to turn this compounded rate into an effective rate, in this case, effective monthly, that is by doing the following.

`r(monthly)=(0.032)/(12) =0,00267`

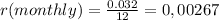
that is 0.267% effective monthly.

Now, we need to take all this annuities to 20 years in the future, which is going to be the present value to use in order to find the amount of moneuy that you can withdraw every month, for 120 months (10 years).

`FutureValue=(A((1+r)^(n) -1))/(r)`

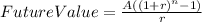
For A = 235.15; r =0,00267; n=240

`FutureValue=(235.15((1+0.00267)^(240) -1))/(0.00267)=78,910.41`

Now, in order to find the amount of money to withdraw for 10 years, every month, we have to use the following equation.

`PresentValue=(A((1+r)^(n)-1) )/(r(1+r)^(n) )`

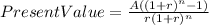
Since the future value 20 years from now is the present value of the annuity we are looking for, all should look like this.

`78,910.41=(A((1+0.00267)^(120)-1) )/(0.00267(1+0.00267)^(120) )`

`78,910.41=A(102.5781087)`

`A=(78,910.41)/(102.5781087) =769.27`

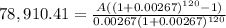
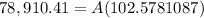
So the answer is a) $769.27

Best of luck.